Abstract—The motion of star systems will cause a Doppler shift on the spectrum, providing valuable insights into the dynamics and characteristics of celestial objects. Astronomical deep space exploration necessitates the use of high-precision astronomical spectrographs to analyze the subtle variations in Doppler shift observed in stellar absorption lines. Astrocombs serve as essential tools for the precision calibration of astronomical spectrographs, playing a crucial role in advancing the fields of cosmology and exoplanet research. As technological fabrication processes undergo continual enhancement, astrocombs undergo iteration. Here we provide a brief overview of astrocombs.
Index Terms—Frequency combs, photonics, cosmology
INTRODUCTION
Spectroscopy is a powerful tool in cosmology research. Due to distinctive spectral signatures of various atoms, this methodology enables the extraction of crucial information such as the chemical composition, temperature, density and so on of celestial objects, through the analysis of light acquired by telescopes[1]. Furthermore, scientists can apply the Doppler shift on spectroscopic data, allowing for the determination of distances to specific celestial objects and the study of the expansion of the universe.
The crux of spectral analysis lies in the utilization of astronomical spectrographs to observe the wavelength shift. To effectively and precisely discern these shifts in the wavelength domain, astronomical spectrographs need to have highly precise wavelength calibration. Astrocombs serve as integral elements for that. As a kind of optical frequency comb, with broadband(from UV to MIR), high-repetition-rate(line spacing < 1GHz) [2] [3], astrocombs can offer broadband spectra of laser lines with precisely known optical frequencies[4], which play a pivotal role in advancing the accuracy of spectroscopy.
ASTROCOMBS
Concepts
The astrocomb, as a variant of optical frequency combs, can be generated by using the mode-locked laser. The description of its optical frequency components can also be characterized through the following comb equations: $$ f_{n}=n*f_{rep}+f_{CEO} $$ In this context, n is an integer number, \(f_{rep}\) represents the laser’s pulse repetition rate, and \(f_{CEO}\) denotes the carrier-envelope offset frequency[5]. Figuratively speaking, \(f_{rep}\) is the distance between combs teeth(modes), while the \(f_{CEO}\) signifies the initial frequency of a frequency combs. Such an equation describes an astrocomb consisting of millions of optical modes, with two degrees of freedom[6]. Through the adjustment of laser source parameters, one can modulate the frequency range of a frequency comb, consequently altering its application scope.
Uniqueness of Astrocomb
The primary distinctions between normal frequency combs and those utilized in astronomy lie in the working wavelength range and the high wavelength precision required. These characteristics are predominantly determined by the specific detection scenarios and requirements in astronomical applications.
Within our galaxy, most stars are Red Dwarfs(M-type mainsequencestarsr, M-V), which are mostly characterised by a cold and red spectrum[7]. At the same time, a G-type mainsequence star(G-V) like our sun, exhibits a more pronounced absorption spectrum, particularly in the blue and ultraviolet (UV) ranges, due to the presence of metal elements in their atmospheres[8]. Indeed, in the domain of observational astronomy, the entire spectral range extending from ultraviolet(> 300nm) to near-infrared(> 2000nm) wavelengths holds significant importance. This imposes elevated requisites on the band range of astrocombs.
Meanwhile, in the field of cosmology, the radial velocity technique is employed to analyze spectral variations in celestial objects, analysing crucial information including orbital distance, mass, and density, among other parameters[4][9][10]. The pursuit of exoplanets greatly benefits from such information, which also underscores the necessity for highresolution optical frequency combs to meet the demands of precise. Returning to the combs equation, it necessitates a narrow width of comb tooth, defined by frep. In a word, the distinctive application requirements imposed by astronomical spectrographs determine specific conditions necessitated for astrocombs, in contrast to conventional frequency combs.
The calibration of a spectrograph typically involves using the spectrograph to measure a known astrocomb 1D spectrum. Subsequently, the extracted ”frequency solutions” from the spectrograph are fitted to the astrocomb spectrum[11]. It is essential to note that astrocomb calibration lines are typically much narrower than the response of the spectrograph, enabling the direct determination of the spectrograph’s response. In practical calibration, we ca vary the repetition frequency of the astrocombs for multiple measurements[12]. By employing this method, one can evaluate the precision of the spectrograph and proceed with the necessary calibration steps. Currently, thorium argon (ThAr) emission lamps are the calibrators for spectrographs used widely[11]. However, these emission lamps exhibit drawbacks such as uneven line spacing, blended atomic lines from various ionic states, and long-term spectral drift. In contrast to these emission lamps, astrocombs present a more stable and precise option for spectrograph calibration, which is particularly advantageous when spectrographs need to operate continuously over extended periods.
REVIEW OF DEMONSTRATED ASTROCOMBS
Filtered Laser Astrocombs
To achieve the desired spectral coverage, one can opt for choosing a specific laser gain medium, complemented by spectral broadening techniques. For the frequency comb resolution, it proves challenging for typical femtosecond laser systems to obtain a repetition rate(\(f_{rep}\)) larger than 10GHz. Indeed, the evolution of mode-locked lasers, which inherently function as frequency combs, has significantly contributed to the field. The simplest and most widely-adopted way to tune mode spacing involves optically filtering the modes of a lower repetition frequency laser (\(f_{rep}\) ≤ 1GHz) in a Fabry–Pérot etalon[13], as illustrated in Fig.1. This straightforward approach directly filters the source combs, which are intrinsically narrow bands. Consequently, the spectral broadening is necessitated to extend the coverage of the astrocomb.
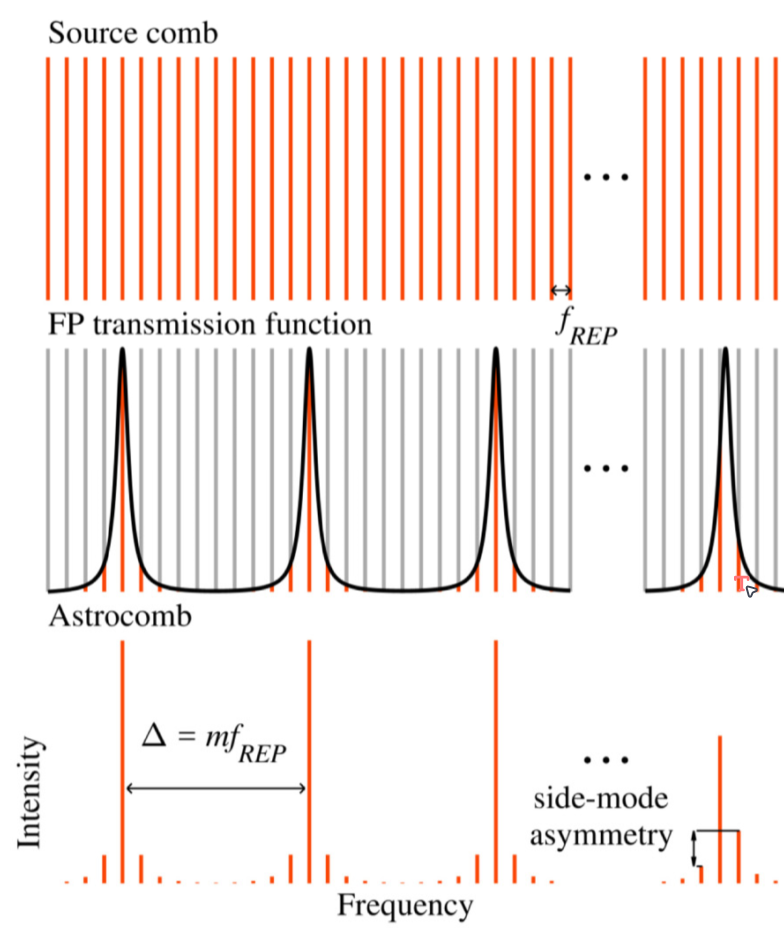
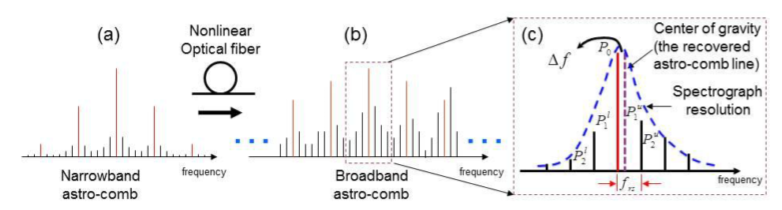
Although spectral broadening can be employed to extend spectrum coverage, optical fitering laser astrocombs predominantly operate within the visible light range. One approach to enhance their performance involves utilizing four-wave mixing cascades, incorporating a few narrow band Fabry–Pérot cavities to amplify the filtered comb signal[14]. Subsequently, these cavities are connected to nonlinear optical fibers to induce power redistribution, leading to a nonlinear spectral broadening and the achievement of broadband coverage. Within the cavities, the implementation of complementary chirped-mirror pairs serves to mitigate the influence of dispersion caused by filtering. However, this optimization approach is accompanied by a degradation of side mode suppression and an increased imbalance of side modes on opposite sides of each primary astrocomb line, which will bring systematic calibration error to the spectrograph. Fig.2 illustrates such a technique.
Solid State Astrocombs System
As previously discussed, the limitations of conventional light sources in providing high-repetition-rate combs necessitate the adoption of alternative approaches such as filtering. This leads to the inception of astrocombs based on highrepetition-rate mode-locked lasers. In this context, the selected gain medium involves Ti:sapphire with Yb doping. Notably, such Yb:ceramic astrocombs have been reported to exhibit mode spacings of up to 10 GHz or even 20 GHz, representing truly attractive parameters for astrocombs[2]. However, the issue of phase noise persists in such kinds of high repetition rate lasers, posing an unresolved challenge. Additionally, the long-term performance characteristics of such systems remain insufficiently understood, impeding broader research and application.
Electro-optical Modulated Astrocombs
An electro-optical modulated astrocomb is a spectrum of lines generated through the electro-optical modulation of a continuous-wave laser source. The system encompasses several pivotal components: initially, a continuous wave is generated by a reference source laser, followed by intense phase modulation to produce sidebands, where the spacing of sidebands is determined by the modulation frequency. Subsequently, the light is coupled to an amplitude modulator driven with the same frequency as the phase modulator and a dispersion compensation unit is employed to shape the pulse. Afterwards, the chirped waveform undergoes compression into picosecond pulses. Finally, the formed pulse is coupled to a second amplification stage (EDFA), and a highly nonlinear fiber (HNLF) is utilized for broadening to create the final astrocombs utilized for spectrography[15]. An example schematic layout for electro-optical modulated astrocombs generation is illustrated in Fig.3.
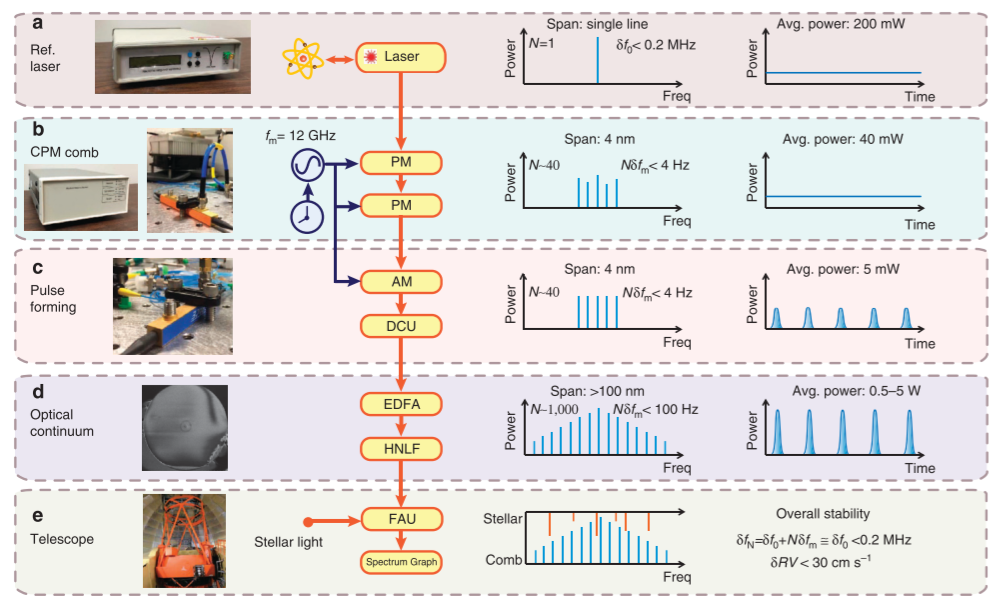
The combination of optical amplification and the incorporation of nonlinear optical effects, in tandem with pulse compression using either fiber or free-space compressors. This results in high-peak-power pulses characterized by pulse durations in the tens-of-femtoseconds range. This makes them well-suited for subsequent nonlinear spectral broadening. However, this approach is not without drawbacks. It comes at the cost of imprinting the inherent phase noise of the microwave source onto the optical comb lines, and for very broadband spectra, it necessitates phase noise suppression in the optical domain.
Moreover, astrocombs generated through this method have been constrained to the 1-2 µm near-infrared band due to the limited availability of commercial modulators with sufficient bandwidth[2].
Astrocombs Based On Photonics Chip
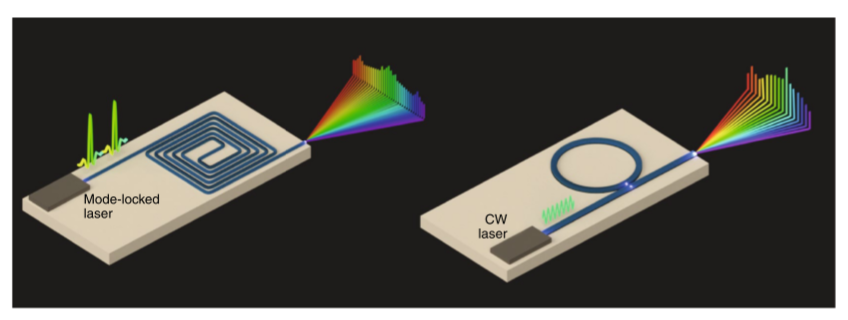
The mode spacing issue in the conventional table-top mode-locked laser astrocombs system, particularly as its source comb spacing is below 1 GHz, poses a significant challenge for spectrograph resolution[16]. Remedies such as Fabry–Pérot modulation introduce system errors, escalating the system’s complexity and cost. Furthermore, the restricted bandwidth poses a limitation on the applicability of table-top modelocked laser astrocomb systems. Consequently, recent advancements in chip-based nonlinear photonics present a more promising prospect for the realization of astrocomb devices. These developments hold the potential for highly compact, portable, robust, and fully integrated astrocomb solutions[17]. Two of the most noteworthy examples capable of producing broad spectra are the processes of super continuum generation (SCG) in optical waveguides and Kerr-comb generation (KCG) in microresonators. In supercontinuum generation (SCG) illustrated in the left part of Fig.4, the pump field comprises a series of ultrashort pulses emitted by a mode-locked laser, itself functioning as a frequency comb. These pulses traverse a waveguide and undergo third-order nonlinear interactions, leading to the extension of the spectrum through parametric four-wave mixing (FWM) processes. Under conditions of robust interaction and appropriate dispersion within the waveguide, the bandwidth of the comb can surpass an octave spanning, with a spacing dictated by the pulse repetition rate of the mode-locked pump laser[17]. The Kerr comb generation (KCG) process subversively adopted a continuous-wave laser as the source, which is illustrated in the right part of Fig.4. The challenging issue of obtaining a high mode spacing frequency pulse laser as a source is circumvented, enabling the use of a more readily available continuous-wave laser source in the fabrication process. In a KCG process, a passive microresonator is optically pumped near a cavity mode by a single-frequency continuous-wave laser. The gain is produced through fourwave mixing (FWM) at other cavity modes. Under conditions of strong nonlinearity and suitable dispersion, a comb is generated, and its spacing is determined by the free spectral range (FSR) of the microresonator. Essentially, this method employs a clock laser that is coupled with the source laser within a ring resonator to achieve the filter frequency effect. This process has been demonstrated to enable the generation of coherent optical frequency combs with a total spectral width that can extend more than an octave[17].
Photonics chip-based platforms provide distinct advantages for supercontinuum generation (SCG) and Kerr comb generation (KCG) compared to fiber-based platforms. These advantages include high effective nonlinearities and the capability to perform robust dispersion engineering across a wide range of pump wavelengths. This feature facilitates phase matching of parametric processes over extremely broad bandwidths. The predominant use of silicon or silicon nitride for waveguide construction leverages the maturity and widespread availability of fabrication techniques associated with silicon-based photonic devices. Currently, photonics chip-based astrocombs enable the generation of low-noise ultra-short femtosecond pulses with repetition rates ( \(f_{rep}\)) that can readily reach and exceed tens of GHz Simultaneously[5]. These platforms demonstrate the potential to cover the entire near-infrared spectrum.
Indeed, while these chip-based approaches offer significant advantages, it is not without its challenges. The integration of fully mode-locked pump lasers with waveguide supercontinuum generation (SCG) devices has proven to be challenging. The difficulties arise from the complexities associated with creating chip-based mode-locked lasers that generate subpicosecond laser pulses, especially when considering electrically pumped configurations. Additionally, in the Kerr comb generation (KCG) process, mode coupling can occur due to frequency degeneracy, and this coupling is strongly influenced by the Raman effect, further complicating the system. While these chip-based astrocombs have demonstrated the potential to cover the entire near-infrared spectral range, with good resolution in a miniaturized and integrated form, the visible band remains challenging for such methods. The generation of astrocombs in the visible band still relies on filtered mode-locked lasers.
CONCLUSION AND OUTLOOK
As of now, the most commonly deployed astrocombs rely on mode-filtered mode-locked lasers. Photonics chip-based astrocombs have also made significant progress in recent years. Currently, near-infrared wavelengths can be effectively covered by higher-resolution astrocombs, even in integrated form. As mentioned earlier, it appears that most stars in the galaxy, characterized by a cold and red spectrum, could be observed using such astrocombs. However, it’s crucial to note that quantity does not necessarily equate to quality. In the quest for finding exoplanets, the visible spectrum, akin to our sun, remains a more pertinent focus[9].
Indeed, the resolution requirements vary for different wavelength ranges, necessitating different repetition frequencies( \(f_{rep}\)) for astrocombs. Currently, this implies the need to integrate multiple astrocombs into a spectrograph to analyze diverse information, introducing cost challenges. In some cases, the cost of astrocombs can even surpass that of the spectrograph itself[13]. With advances in mode-locked lasers, the construction of higher repetition frequency lasers becomes possible, which also makes high-resolution astrocombs in the visible light band possible.
ACKNOWLEDGMENT
The author would like to thank Patrick Uros Nenezic, Khaled Abo-ElSoud and Tom Vanmaele, those who reviewed this paper and gave enlightening comments. Sincere gratitude should also go to learned Professor Wim Bogaerts and Professor Stephane Clemmen, who gave great help during the whole studying process.
References
[1] T. Udem, R. Holzwarth, and T. W. Hansch, “Optical frequency metrology,” Nature, vol. 416, no. 6877, pp. 233–237, 2002.
[2] T. Herr and R. A. McCracken, “Astrocombs: recent advances,” IEEE Photonics Technology Letters, vol. 31, no. 23, pp. 1890–1893, 2019.
[3] G. Chang, C.-H. Li, D. F. Phillips, R. L. Walsworth, and F. X. K¨artner, “Toward a broadband astro-comb: effects of nonlinear spectral broadening in optical fibers,” Optics Express, vol. 18, no. 12, pp. 12736– 12747, 2010.
[4] A. J. Benedick, G. Chang, J. R. Birge, L.-J. Chen, A. G. Glenday, C.-H. Li, D. F. Phillips, A. Szentgyorgyi, S. Korzennik, G. Furesz, et al., “Visible wavelength astro-comb,” Optics express, vol. 18, no. 18, pp. 19175–19184, 2010.
[5] E. Obrzud, M. Rainer, A. Harutyunyan, M. H. Anderson, J. Liu, M. Geiselmann, B. Chazelas, S. Kundermann, S. Lecomte, M. Cecconi, et al., “A microphotonic astrocomb,” Nature Photonics, vol. 13, no. 1, pp. 31–35, 2019.
[6] T. Fortier and E. Baumann, “20 years of developments in optical frequency comb technology and applications,” Communications Physics, vol. 2, no. 1, p. 153, 2019.
[7] S. W. Jha, K. Maguire, and M. Sullivan, “Observational properties of thermonuclear supernovae,” Nature Astronomy, vol. 3, no. 8, pp. 706– 716, 2019.
[8] D. F. Phillips, A. G. Glenday, X. Dumusque, N. Buchschacher, A. C. Cameron, M. Cecconi, D. Charbonneau, R. Cosentino, A. Ghedina, R. Haywood, et al., “An astro-comb calibrated solar telescope to search for the radial velocity signature of venus,” in Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, vol. 9912, pp. 2163–2170, SPIE, 2016.
[9] M.-G. Suh, X. Yi, Y.-H. Lai, S. Leifer, I. S. Grudinin, G. Vasisht, E. C. Martin, M. P. Fitzgerald, G. Doppmann, J. Wang, et al., “Searching for exoplanets using a microresonator astrocomb,” Nature Photonics, vol. 13, no. 1, pp. 25–30, 2019.
[10] F. Zhao, G. Zhao, Y. Liu, L. Wang, H. Wang, H. Li, H. Ye, Z. Hao, D. Xiao, J. Zhang, et al., “Statistical modelling of an astro-comb for high-precision radial velocity observation,” Monthly Notices ofthe Royal Astronomical Society, vol. 482, no. 1, pp. 1406–1416, 2019.
[11] D. F. Phillips, A. Glenday, C.-H. Li, G. Furesz, A. J. Benedick, G. N. Chang, L.-J. Chen, S. Korzennik, D. Sasselov, F. X. Kaertner, et al., “Calibration of an echelle spectrograph with an astro-comb: a laser frequency comb with very high repetition rate,” in Ground-based and Airborne Instrumentation for Astronomy IV, vol. 8446, pp. 1188–1197, SPIE, 2012.
[12] A. Ravi, D. F. Phillips, M. Beck, L. L. Martin, M. Cecconi, A. Ghedina, E. Molinari, A. Bartels, D. Sasselov, A. Szentgyorgyi, et al., “Astrocomb calibrator and spectrograph characterization using a turn-key laser frequency comb,” Journal of Astronomical Telescopes, Instruments, and Systems, vol. 3, no. 4, pp. 045003–045003, 2017.
[13] R. A. McCracken, J. M. Charsley, and D. T. Reid, “A decade of astrocombs: recent advances in frequency combs for astronomy,” Optics Express, vol. 25, no. 13, pp. 15058–15078, 2017.
[14] A. G. Glenday, C.-H. Li, N. Langellier, G. Chang, L.-J. Chen, G. Furesz, A. A. Zibrov, F. K¨artner, D. F. Phillips, D. Sasselov, et al., “Operation of a broadband visible-wavelength astro-comb with a high-resolution astrophysical spectrograph,” Optica, vol. 2, no. 3, pp. 250–254, 2015.
[15] X. Yi, K. Vahala, J. Li, S. Diddams, G. Ycas, P. Plavchan, S. Leifer, J. Sandhu, G. Vasisht, P. Chen, et al., “Demonstration of a near-ir line-referenced electro-optical laser frequency comb for precision radial velocity measurements in astronomy,” Nature Communications, vol. 7, no. 1, p. 10436, 2016.
[16] Y. Ma, F. Meng, Y. Liu, F. Zhao, G. Zhao, A. Wang, and Z. Zhang, “Visible astro-comb filtered by a passively stabilized fabry-perot cavity,” Review of Scientific Instruments, vol. 90, no. 1, 2019.
[17] A. L. Gaeta, M. Lipson, and T. J. Kippenberg, “Photonic-chip-based frequency combs,” Nature Photonics, vol. 13, no. 3, pp. 158–169, 2019.